clana: Estatística Aplicada à Hidrometria

Aplicação de modelos de regressão múltipla para solução de dados faltantes em séries históricas de dados hidrométricos.

Gráfico de dispersão de um dos modelos abordados.

Introdução

Este trabalho investiga a aplicabilidade de modelos de regressão múltipla no preenchimento de dados faltantes nas séries históricas de dados hidrométricos da Agência Nacional de Águas (ANA).

A ANA é uma entidade do governo brasileiro responsável pela realização de estudos, pesquisas, elaboração e fiscalização de normas reguladoras relacionadas aos recursos hídricos e ao saneamento básico (BRASIL, 2000).

A ANA disponibiliza dados através de um sistema público, o Sistema Nacional de Informações sobre Recursos Hídricos (SNIRH), onde é possível acessar medições de níveis fluviais, vazões, chuvas, clima, qualidade da água e sedimentos. As medições são coletadas por diferentes instituições e empresas ligadas à Rede Hidrometeorológica Nacional, coordenada pela ANA. Em 2018, a rede contava com 4641 pontos de monitoramento (“Portal HidroWeb”, 2023).

O principal conjunto de dados utilizado foi uma série histórica referente à estação de coleta de dados Jacareí (Código 58110002), localizada no Rio Paraíba do Sul e operada pelo Serviço Geológico do Brasil. A série consiste de 962 observações ao longo dos anos 2000 a 2023.

A filtragem dos dados disponibilizados pelo termo “Jacareí” retornou um total de 33 resultados, tabulados abaixo por seus prefixos:

Nº	Categoria	Arquivos
1	chuvas	12
2	cotas	5
3	curvadescarga	2
4	PerfilTransversal	2
5	qualagua	3
6	ResumoDescarga	4
7	sedimentos	1
8	vazoes	4
Σ	Total	33

Em sua maior parte, tratam-se de dados de chuvas e cotas. O termo cotas refere-se aos níveis de água dos rios (ANA, 2021).

As observações são distribuídas em 78 colunas, 62 delas para cada um dos 31 dias do mês e 31 informações de status para o dia respectivo:

• Cotas: Cota01 Cota02 (…) Cota30 Cota31

• Status: Cota01Status Cota02Status (…) Cota30Status Cota31Status

Antes destas 62 colunas, as primeiras 16 são:

• EstacaoCodigo NivelConsistencia Data Hora MediaDiaria TipoMedicaoCotas Maxima Minima Media DiaMaxima DiaMinima MaximaStatus MinimaStatus MediaStatus MediaAnual MediaAnualStatus

O significado de algumas destas variáveis é dado no topo de cada arquivo disponibilizado pelo sistema Hidroweb:

NivelConsistencia: 1 = Bruto, 2 = Consistido
MediaDiaria: 0 = Não, 1 = Sim
TipoMedicaoCotas: 1 = Escala, 2 = Linígrafo, 3 = Data Logger
Status: 0 = Branco, 1 = Real, 2 = Estimado, 3 = Duvidoso, 4 = Régua Seca

Esta informação, que aparece antes dos dados estruturados, foi removida nos arquivos utilizados para análise neste trabalho, já que dificulta a leitura por ferramentas computacionais. O arquivo original foi preservado e acompanha os conjuntos processados.

Este relatório foi elaborado utilizando R como ferramenta principal, uma linguagem de programação voltada à estatística. Para publicação, foi utilizado também o sistema de cadernos Quarto, parte do mesmo ecossistema.

Parte dos conceitos utilizados foi desenvolvida paralelamente no trabalho clana, um estudo sobre Estruturas de Dados onde um outro conjunto da agência foi utilizado para o desenvolvimento de uma aplicação capaz de identificar e preencher lacunas usando modelos de regressão linear simples.

Visão geral

Escopo do projeto

Objetivo	Demonstrar a aplicabilidade de algoritmos de regressão linear múltipla na solução de dados faltantes em séries históricas de dados hidrométricos da Agência Nacional de Águas
Problema	Determinar programaticamente quais variáveis possuem correlações fortes
Métrica	Coeficiente de correlação
Público	Pessoas pesquisadoras, estudantes e profissionais da área de hidrometria, geometeorologia e gestão de recursos hídricos
Dados	cotas_C_58110002.csv

Conjunto de dados utilizado:

AGÊNCIA NACIONAL DE ÁGUAS. cotas_C_58110002. Brasília, 2018. Disponível em: https://www.snirh.gov.br/hidroweb/. Acesso em: 29 jun. 2023

Levantamento

Resultados da filtragem para Jacareí

Código	Estação	Tipo de dado
58110001	JACAREÍ - RÉGUA DA MARGEM	Fluviométrica
58110002	JACAREÍ	Fluviométrica
58096000	UHE SANTA BRANCA JUSANTE	Fluviométrica
58110000	UHE SANTA BRANCA JACAREÍ	Fluviométrica
58044000	BAIRRO RIO COMPRIDO	Fluviométrica
58138000	BAIRRO REMEDINHO	Fluviométrica
58110010	JACAREÍ	Fluviométrica
58138500	PTE. ACESSO RES. JAQUARI (próx. Brahma)	Fluviométrica

O coeficiente de correlação, aqui obtido programaticamente para encontrar relações fortes entre as diferentes variáveis, foi utilizado como a métrica norteadora deste estudo através de uma matriz de correlação.

Carregamento

Nesta etapa, os dados foram carregados e preparados para o processamento.

O arquivo de dados original é disponibilizado no formato csv, com vírgulas separando casas decimais e ponto e vírgula separando as colunas.

Serão utilizadas as bibliotecas tidyverse e janitor para limpar e fazer o processamento inicial dos dados:

library(tidyverse)
library(janitor)

O termo cotas foi adotado para referir-se ao conjunto de dados no código.

cotas <- read_delim("dados/cotas_C_58110002_headless.csv", delim=";")

Warning: One or more parsing issues, call `problems()` on your data frame for details,
e.g.:
  dat <- vroom(...)
  problems(dat)

Rows: 962 Columns: 78
── Column specification ────────────────────────────────────────────────────────
Delimiter: ";"
chr  (3): Data, Hora, Cota31Status
dbl (75): EstacaoCodigo, NivelConsistencia, MediaDiaria, TipoMedicaoCotas, M...

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

Limpeza

Pela saída da importação é possível ver que há problemas. A mesma mensagem indica como listá-los:

problems(cotas)

ABCDEFGHIJ0123456789

row <int>	col <int>	expected <chr>	actual <chr>
2	79	78 columns	79 columns
3	79	78 columns	79 columns
4	79	78 columns	79 columns
5	79	78 columns	79 columns
6	79	78 columns	79 columns
7	79	78 columns	79 columns
8	79	78 columns	79 columns
9	79	78 columns	79 columns
10	79	78 columns	79 columns
11	79	78 columns	79 columns

Next

123456

...

97

Previous

1-10 of 962 rows | 1-4 of 5 columns

Parece que cada linha é terminada com um caracter ; extra.

Será portanto necessário limpar este caracter da última coluna e alterar o tipo para numérico:

cotas$Cota31Status <- as.numeric(gsub(";$", "", cotas$Cota31Status))

O conjunto carregado agora possui uma estrutura uniforme, ainda que com muitas lacunas:

Código

cotas |> 
  filter(
    grepl("01/04/2022", Data)
  )

ABCDEFGHIJ0123456789

EstacaoCodigo <dbl>	NivelConsistencia <dbl>	Data <chr>	Hora <chr>
58110002	1	01/04/2022	01/01/1900 07:00:00
58110002	1	01/04/2022	01/01/1900 17:00:00
58110002	1	01/04/2022	NA

3 rows | 1-4 of 78 columns

Acima, uma filtragem demonstrativa das observações referentes ao mês de abril de 2022.

Cabeçalhos

Os cabeçalhos do arquivo original foram processados automaticamente, e não possuem caracteres especiais ou espaços:

colnames(cotas)

 [1] "EstacaoCodigo"     "NivelConsistencia" "Data"             
 [4] "Hora"              "MediaDiaria"       "TipoMedicaoCotas" 
 [7] "Maxima"            "Minima"            "Media"            
[10] "DiaMaxima"         "DiaMinima"         "MaximaStatus"     
[13] "MinimaStatus"      "MediaStatus"       "MediaAnual"       
[16] "MediaAnualStatus"  "Cota01"            "Cota02"           
[19] "Cota03"            "Cota04"            "Cota05"           
[22] "Cota06"            "Cota07"            "Cota08"           
[25] "Cota09"            "Cota10"            "Cota11"           
[28] "Cota12"            "Cota13"            "Cota14"           
[31] "Cota15"            "Cota16"            "Cota17"           
[34] "Cota18"            "Cota19"            "Cota20"           
[37] "Cota21"            "Cota22"            "Cota23"           
[40] "Cota24"            "Cota25"            "Cota26"           
[43] "Cota27"            "Cota28"            "Cota29"           
[46] "Cota30"            "Cota31"            "Cota01Status"     
[49] "Cota02Status"      "Cota03Status"      "Cota04Status"     
[52] "Cota05Status"      "Cota06Status"      "Cota07Status"     
[55] "Cota08Status"      "Cota09Status"      "Cota10Status"     
[58] "Cota11Status"      "Cota12Status"      "Cota13Status"     
[61] "Cota14Status"      "Cota15Status"      "Cota16Status"     
[64] "Cota17Status"      "Cota18Status"      "Cota19Status"     
[67] "Cota20Status"      "Cota21Status"      "Cota22Status"     
[70] "Cota23Status"      "Cota24Status"      "Cota25Status"     
[73] "Cota26Status"      "Cota27Status"      "Cota28Status"     
[76] "Cota29Status"      "Cota30Status"      "Cota31Status"     

Não foi necessária qualquer limpeza e eles puderam ser mantidos como no original, o que trouxe facilidade na verificação cruzada com o conjunto original e ferramentas auxiliares tais como planilhas.

Análise

Abaixo obteve-se uma listagem de quantas lacunas há em cada coluna:

Código

# obtém a quantidade de entradas nulas em cada coluna 
total_lacunas <- colSums(is.na(cotas))

# filtra colunas sem valores nulos
total_lacunas <- total_lacunas[total_lacunas > 0]

# ordena os resultados de forma decrescente 
total_lacunas <- total_lacunas[order(total_lacunas, decreasing = TRUE)]

as_tibble(
 enframe(total_lacunas, name = "column", value = "n"))

ABCDEFGHIJ0123456789

column <chr>	n <dbl>
MediaAnual	782
Hora	444
Cota31	440
Cota31Status	151
Cota30	145
Cota29Status	135
Cota01Status	134
Cota02Status	134
Cota03Status	134
Cota04Status	134

Next

123456

...

8

Previous

1-10 of 72 rows

Correlação

Usando a função cor() é possível chegar a uma matriz de coeficientes de correlação entre cada variável:

Código

# TODO: Considerar o desvio padrão

library(dplyr)
library(Matrix)

matriz <- cotas |>
  select_if(is.numeric) |>
  cor(use = "pairwise.complete.obs") |>
  as_tibble() 

matriz |>
  add_column(Coluna = colnames(cotas)
    [sapply(cotas, is.numeric)], .before = 1)

ABCDEFGHIJ0123456789

Coluna <chr>	EstacaoCodigo <dbl>	NivelConsistencia <dbl>	MediaDiaria <dbl>
EstacaoCodigo	NA	NA	NA
NivelConsistencia	NA	1.0000000000	0.51821057
MediaDiaria	NA	0.5182105745	1.00000000
TipoMedicaoCotas	NA	NA	NA
Maxima	NA	-0.0694707626	-0.04217493
Minima	NA	-0.0411037066	-0.02901073
Media	NA	-0.0505854671	-0.03485165
DiaMaxima	NA	0.0504187583	0.03150562
DiaMinima	NA	0.0005889856	-0.00145271
MaximaStatus	NA	0.8900153792	0.49668630

Next

123456

...

8

Previous

1-10 of 76 rows | 1-4 of 77 columns

A matriz de correlação obtida acima usa um método de correlação em pares para a covariância, parâmetro que indica o grau de interdependência linear entre duas variáveis em relação às suas médias.

Com a opção pairwise.complete.obs, são considerados apenas os pares onde nenhum dos dois valores é nulo. Como desvantagem, ela pode reduzir demais o tamanho da amostra quando há uma quantidade grande de valores nulos.

Temos agora valores nulos apenas para as colunas e linhas onde todos os valores eram nulos originalmente. Para removê-los:

matriz <- remove_empty(matriz)

A documentação do pacote stats, ao qual pertence a função cor() utilizada acima, explica especificamente sobre a opção de completação de lacunas em pares:

“[for pairwise.complete.obs] the correlation or covariance between each pair of variables is computed using all complete pairs of observations on those variables. This can result in covariance or correlation matrices which are not positive semi-definite, as well as NA entries if there are no complete pairs for that pair of variables.” (R CORE TEAM, 2019)

Validação do instrumento

A documentação também menciona que esta opção, em tradução livre, “pode resultar em matrizes de covariância ou correlação que não são positivas semi-definidas”, o que tem implicações que prejudicam a aplicabilidade da matriz na análise estatística.

Para compreender melhor o conceito de uma matriz positiva semi-definida (PSD) e aferir o efeito da escolha do método pairwise.complete.obs, foram utilizados duas técnicas de decomposição para verificar se a matriz é ou não uma matriz PSD.

Método de decomposição de autovalores

Código

matriz_tipada <- as.matrix(matriz)
autovalores <- eigen(matriz_tipada)$values

if(all(autovalores >= 0)) {
  print("A matriz é PSD")
} else {
  print("A matriz não é PSD")
}

[1] "A matriz não é PSD"

Método de decomposição de Cholesky

Código

triangular_inferior <- tryCatch(chol(matriz), error = function(e) NULL)

if(is.null(triangular_inferior)) {
  print("A matriz não é PSD")
} else {
  if(all.equal(matriz, crossprod(triangular_inferior))) {
    print("A matriz é PSD")
  }
}

[1] "A matriz não é PSD"

Os resultados mostram que a matriz obtida não é positiva semi-definida. Testes com a opção na.or.complete também não resultaram em uma matriz PSA.

Observando a matriz de autovalores, temos:

eigen(matriz)$values

 [1]  3.304671e+01  2.677692e+01  3.976231e+00  1.868539e+00  1.084119e+00
 [6]  8.337463e-01  8.183780e-01  6.740758e-01  5.365000e-01  3.227351e-01
[11]  3.085505e-01  2.171506e-01  1.817382e-01  1.622910e-01  1.322591e-01
[16]  1.272485e-01  1.165717e-01  8.765272e-02  8.596270e-02  6.983907e-02
[21]  6.669530e-02  6.525508e-02  5.276238e-02  5.167361e-02  4.577009e-02
[26]  4.220613e-02  4.029004e-02  3.450093e-02  3.342940e-02  2.778568e-02
[31]  2.680202e-02  2.403391e-02  2.206614e-02  1.898203e-02  1.804426e-02
[36]  1.680097e-02  1.493449e-02  1.384304e-02  1.293349e-02  1.227241e-02
[41]  1.090765e-02  1.013699e-02  8.931990e-03  8.324636e-03  8.039344e-03
[46]  7.093028e-03  6.553614e-03  6.112212e-03  5.389511e-03  4.489292e-03
[51]  4.464281e-03  3.555311e-03  3.313878e-03  2.388201e-03  2.022481e-03
[56]  1.866073e-03  8.053837e-04  4.753483e-16  3.391994e-16  1.514189e-16
[61]  4.503450e-17 -9.757525e-17 -1.097625e-16 -2.994173e-06 -3.754538e-05
[66] -2.829942e-03 -3.100618e-03 -5.936686e-03 -1.285535e-02 -3.209864e-02
[71] -4.439433e-02 -6.143459e-02

Parece que os autovalores negativos estão todos após a posição 62.

Recorte

Foi realizado um recorte utilizando apenas os dados referentes às cotas de cada 31 dias:

Código

recorte <- cotas |>
  select(Cota01:Cota31) |>
  drop_na()
 
recorte

ABCDEFGHIJ0123456789

Cota01 <dbl>	Cota02 <dbl>	Cota03 <dbl>	Cota04 <dbl>	Cota05 <dbl>	Cota06 <dbl>	Cota07 <dbl>	Cota08 <dbl>	Cota09 <dbl>	Cota10 <dbl>
78	78	78	78	75	74	74	71	72	74
72	71	70	68	55	57	60	74	71	70
75	75	74	73	65	66	67	73	72	72
119	119	119	113	106	105	105	106	106	106
119	119	119	119	105	105	105	106	106	106
119	119	119	106	106	105	105	105	106	106
167	167	168	168	180	180	180	180	188	188
167	167	168	168	180	180	180	180	188	188
167	167	168	168	180	180	180	180	188	188
158	158	158	158	158	162	162	162	162	162

Next

123456

...

52

Previous

1-10 of 514 rows | 1-10 of 31 columns

Em seguida, o recorte foi limpo de colunas ou linhas contendo campos vazios.

Código

matriz_recorte <- recorte |>
  select_if(is.numeric) |>
  cor(use = "na.or.complete") |>
  as_tibble() 

matriz_recorte

ABCDEFGHIJ0123456789

Cota01 <dbl>	Cota02 <dbl>	Cota03 <dbl>	Cota04 <dbl>	Cota05 <dbl>	Cota06 <dbl>	Cota07 <dbl>
1.0000000	0.9843837	0.9749178	0.9666425	0.9558252	0.9559924	0.9448886
0.9843837	1.0000000	0.9843187	0.9745932	0.9596469	0.9606027	0.9493034
0.9749178	0.9843187	1.0000000	0.9892490	0.9636828	0.9600585	0.9505056
0.9666425	0.9745932	0.9892490	1.0000000	0.9783869	0.9679394	0.9521808
0.9558252	0.9596469	0.9636828	0.9783869	1.0000000	0.9876378	0.9661084
0.9559924	0.9606027	0.9600585	0.9679394	0.9876378	1.0000000	0.9793599
0.9448886	0.9493034	0.9505056	0.9521808	0.9661084	0.9793599	1.0000000
0.9381880	0.9413465	0.9393227	0.9414484	0.9586847	0.9698278	0.9848786
0.9336140	0.9330056	0.9281905	0.9301548	0.9498871	0.9638331	0.9775429
0.9310289	0.9309882	0.9264741	0.9288885	0.9485362	0.9619393	0.9712373

Next

1234

Previous

1-10 of 31 rows | 1-7 of 31 columns

A recontagem de valores nulos mostra que não restaram mais lacunas:

Código

# obtém a quantidade de entradas nulas em cada coluna 
lacunas <- colSums(is.na(matriz_recorte))

# filtra colunas sem valores nulos
lacunas <- lacunas[lacunas > 0]

# ordena os resultados de forma decrescente 
lacunas <- lacunas[order(lacunas, decreasing = TRUE)]

as_tibble(enframe(lacunas, name = "column", value = "n"))

ABCDEFGHIJ0123456789

column <chr>	n <dbl>

0 rows

Método de decomposição de autovalores

O novo recorte foi testado com sucesso pela decomposição de autovalores:

Código

tryCatch( autovalores <- eigen(matriz_recorte)$values , error = function(e) NULL)

if(is.null(autovalores)) {
  print("Erro:")
  print(e)
} else {
  if(all(autovalores >= 0)) {
    print("A matriz é PSD")
  } else {
    print("A matriz não é PSD")
  }
}

[1] "A matriz é PSD"

Embora com este recorte seja possível um resultado positivo usando a técnica de verificação pela decomposição de autovalores, o fato da matriz não ser simétrica torna impossível realizar a segunda etapa necessária ao teste de decomposição de Cholesky.

O teste abaixo verifica se a matriz é simétrica:

Código

matriz_recorte <- as.matrix(matriz_recorte)

if (isSymmetric(matriz_recorte)) {
  print("A matriz é simétrica")
} else {
  print("A matriz não é simétrica")
}

[1] "A matriz não é simétrica"

Uma solução para o problema é completar a forma simétrica da matriz pela sua transposta.

Método de decomposição de Cholesky com a matriz completada

Código

# obtém a matriz simétrica somando-a com a transposta e dividindo por 2
matriz_simetrica <- (matriz_recorte + t(matriz_recorte)) / 2
triangular_inferior <- tryCatch(chol(matriz_simetrica), error = function(e) NULL)

triangular_superior <- row(triangular_inferior) > col(triangular_inferior)
all(triangular_inferior[triangular_superior] == 0)

[1] TRUE

Foram levantados ainda os seguintes testes adicionais, que também confirmaram a matriz como PSD:

Teste por decomposição em valores singulares

Código

decomposicao <- svd(matriz_recorte)
all(decomposicao$d >= 0)

[1] TRUE

Teste pela forma quadrática

Código

n_colunas = ncol(matriz_recorte)

x <- sample(-9:9, n_colunas, replace = TRUE)

while (all(x == 0)) {  
  x <- sample(-9:9, n_colunas, replace = TRUE)
}

resultado <- TRUE
for (i in 1:n_colunas) {
  if (t(x) %*% matriz_recorte %*% x < 0) {
    resultado <- FALSE
    break
  }
}

resultado

[1] TRUE

Aplicação

Utilizando esta região, podemos fitlrar o conjunto original para ver como ela é incluindo suas lacunas.

Código

cotas |>
  select(Cota01:Cota31)

ABCDEFGHIJ0123456789

Cota01 <dbl>	Cota02 <dbl>	Cota03 <dbl>	Cota04 <dbl>	Cota05 <dbl>	Cota06 <dbl>	Cota07 <dbl>	Cota08 <dbl>	Cota09 <dbl>	Cota10 <dbl>
NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
NA	NA	NA	NA	NA	NA	NA	NA	NA	NA
85	82	82	83	84	82	81	82	83	84
81	82	83	84	82	82	81	82	83	84
88	82	81	82	85	82	81	82	83	84
78	78	78	78	75	74	74	71	72	74
72	71	70	68	55	57	60	74	71	70
75	75	74	73	65	66	67	73	72	72
119	119	119	113	106	105	105	106	106	106

Next

123456

...

97

Previous

1-10 of 962 rows | 1-10 of 31 columns

Podemos encontrar diversas áreas onde o modelo desenvolvido pode ser testado. Por exemplo, a região abaixo:

Código

cotas |> 
  select(Cota05:Cota16) |>
  slice(745:755)

ABCDEFGHIJ0123456789

Cota05 <dbl>	Cota06 <dbl>	Cota07 <dbl>	Cota08 <dbl>	Cota09 <dbl>	Cota10 <dbl>	Cota11 <dbl>	Cota12 <dbl>	Cota13 <dbl>	Cota14 <dbl>
34	51	46	33	28	27	28	37	48	43
34	28	28	28	26	24	23	23	23	22
33	36	NA	NA	NA	NA	NA	NA	19	25
37	35	NA	NA	NA	NA	NA	19	19	22
35	36	NA	NA	NA	NA	NA	NA	19	24
108	108	108	108	108	108	108	108	108	110
108	108	108	108	108	108	108	108	108	113
108	108	108	108	108	108	108	108	108	112
65	74	74	73	74	72	68	67	67	67
69	74	74	73	74	71	67	67	67	67

Next

12

Previous

1-10 of 11 rows | 1-10 of 12 columns

Esta região corresponde aos dias 7 a 12 de abril de 2022.

Na tabela abaixo, vemos a mesma matriz de correlação com uma coluna extra à frente que facilita verificar a correlação entre as observações mostradas no intervalo.

Código

matriz_df <- matriz_recorte |>
  as.data.frame()

matriz_df |>
  add_column(Colunas = colnames(matriz_recorte), .before = 1)

ABCDEFGHIJ0123456789

Colunas <chr>	Cota01 <dbl>	Cota02 <dbl>	Cota03 <dbl>	Cota04 <dbl>	Cota05 <dbl>	Cota06 <dbl>
Cota01	1.0000000	0.9843837	0.9749178	0.9666425	0.9558252	0.9559924
Cota02	0.9843837	1.0000000	0.9843187	0.9745932	0.9596469	0.9606027
Cota03	0.9749178	0.9843187	1.0000000	0.9892490	0.9636828	0.9600585
Cota04	0.9666425	0.9745932	0.9892490	1.0000000	0.9783869	0.9679394
Cota05	0.9558252	0.9596469	0.9636828	0.9783869	1.0000000	0.9876378
Cota06	0.9559924	0.9606027	0.9600585	0.9679394	0.9876378	1.0000000
Cota07	0.9448886	0.9493034	0.9505056	0.9521808	0.9661084	0.9793599
Cota08	0.9381880	0.9413465	0.9393227	0.9414484	0.9586847	0.9698278
Cota09	0.9336140	0.9330056	0.9281905	0.9301548	0.9498871	0.9638331
Cota10	0.9310289	0.9309882	0.9264741	0.9288885	0.9485362	0.9619393

Next

1234

Previous

1-10 of 31 rows | 1-7 of 32 columns

Modelo demonstrativo

Usando a função nativa em R para criar modelos de regressão linear, podemos criar um modelo utilizando duas ou mais variáveis. Para a coluna 7, podemos usar as colunas completas mais próximas, 6 e 5, que possuem coeficientes de correlação maiores.

Código

model = lm(Cota07~Cota06 + Cota05, data = matriz_df)

O modelo retornado contém diferentes parâmetros para esta correlação específica:

Call:
lm(formula = Cota07 ~ Cota06 + Cota05, data = matriz_df)

Residuals:
       Min         1Q     Median         3Q        Max 
-0.0233749 -0.0020224  0.0001333  0.0019238  0.0148345 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.09288    0.05660   1.641    0.112    
Cota06       1.95404    0.21484   9.095 7.48e-10 ***
Cota05      -1.05726    0.17802  -5.939 2.16e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.006388 on 28 degrees of freedom
Multiple R-squared:  0.8949,    Adjusted R-squared:  0.8874 
F-statistic: 119.2 on 2 and 28 DF,  p-value: 2.01e-14

É possível destacar, por exemplo, os coeficientes:

(Intercept)      Cota06      Cota05 
  0.0928818   1.9540448  -1.0572619 

E $r^2$ para a correlação múltipla entre as variáveis Cota07, Cota06 e Cota05:

[1] 0.8948865

Código

library(ggplot2)

ggplot(matriz_df, aes(x = Cota07, y = Cota06)) +
  geom_point() +
  geom_smooth(method = "lm", formula = y ~ x, se = FALSE, color = "darkgreen") +
  labs(x = "Cota 07", y = "Cota 06") +
  annotate("text", x = max(matriz_df$Cota07), y = max(matriz_df$Cota06),
  label = paste("r:", round(cor(matriz_df$Cota07, matriz_df$Cota06), 2)),
  hjust = 1, vjust = 1)

Plotagem para a correlação entre Cota07 e Cota06. As variáveis apresentaram uma correlação positiva de 87%

Código

library(ggplot2)

ggplot(matriz_df, aes(x = Cota07, y = Cota01)) +
  geom_point() +
  geom_smooth(method = "lm", formula = y ~ x, se = FALSE, color = "darkgreen") +
  labs(x = "Cota 07", y = "Cota 01") +
  annotate("text", x = max(matriz_df$Cota07), y = max(matriz_df$Cota01),
  label = paste("r:", round(cor(matriz_df$Cota07, matriz_df$Cota01), 2)),
  hjust = 1, vjust = 1)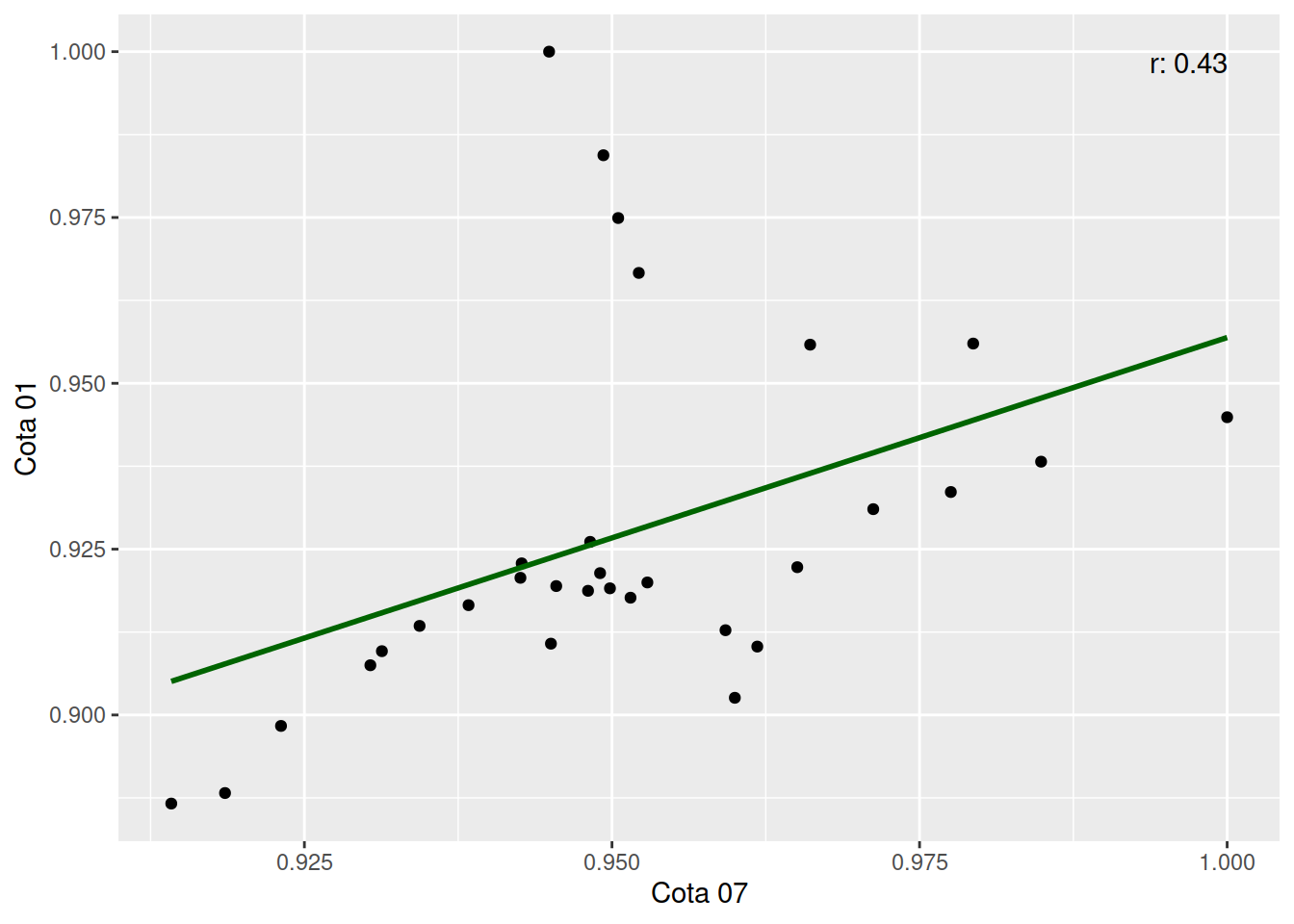

Plotagem demonstrativa para uma entre duas medições distantes, Cota01 e Cota07. A correlação encontrada foi de apenas 43%

Código

library(ggplot2)

ggplot(matriz_df, aes(x = Cota03, y = Cota04)) +
  geom_point() +
  geom_smooth(method = "lm", formula = y ~ x, se = FALSE, color = "darkgreen") +
  labs(x = "Cota 03", y = "Cota 04") +
  annotate("text", x = max(matriz_df$Cota03), y = max(matriz_df$Cota04),
  label = paste("r:", round(cor(matriz_df$Cota03, matriz_df$Cota04), 2)),
  hjust = 1, vjust = 1)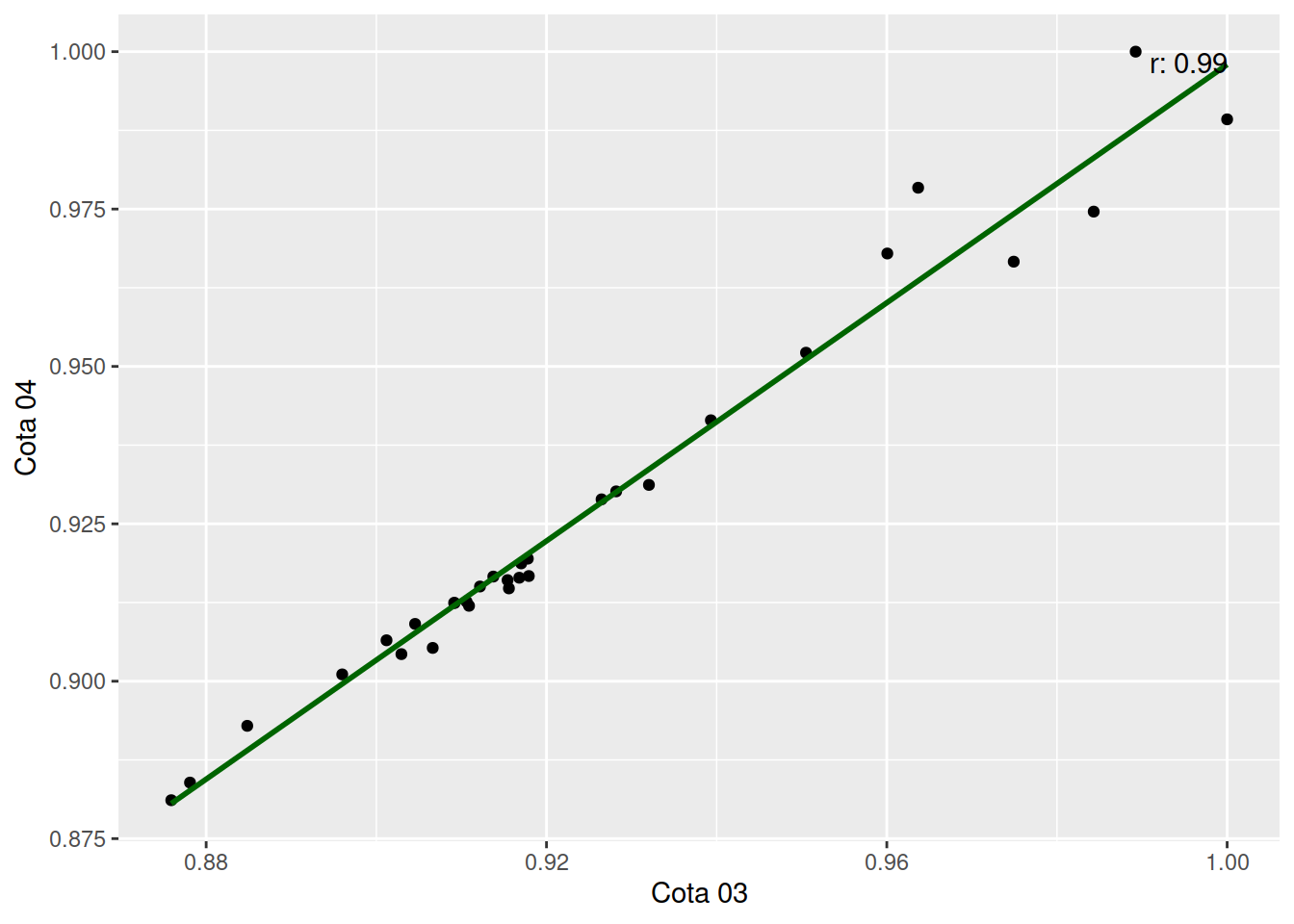

Dispersão para Cota03 e Cota04, com correlação de 99%, uma das maiores encontradas na matriz de correlação. Os padrões observáveis na matriz mostram que medições em dias próximos exibem um padrão linear de mudança.

Conclusão

Para cenários onde os níveis dos rios não passam por mudanças bruscas, a regressão linear pode ser um instrumento eficaz na previsão de valores faltantes, em especial onde há dados em dias contíguos que podem ser usados na construção do modelo.

Como o estudo tomou como principal métrica os coeficientes de correlação, numericamente os dados mais sintéticos sobre o que foi observado estão na matriz de correlação obtida:

ABCDEFGHIJ0123456789

Cota01 <dbl>	Cota02 <dbl>	Cota03 <dbl>	Cota04 <dbl>	Cota05 <dbl>	Cota06 <dbl>	Cota07 <dbl>
1.0000000	0.9843837	0.9749178	0.9666425	0.9558252	0.9559924	0.9448886
0.9843837	1.0000000	0.9843187	0.9745932	0.9596469	0.9606027	0.9493034
0.9749178	0.9843187	1.0000000	0.9892490	0.9636828	0.9600585	0.9505056
0.9666425	0.9745932	0.9892490	1.0000000	0.9783869	0.9679394	0.9521808
0.9558252	0.9596469	0.9636828	0.9783869	1.0000000	0.9876378	0.9661084
0.9559924	0.9606027	0.9600585	0.9679394	0.9876378	1.0000000	0.9793599
0.9448886	0.9493034	0.9505056	0.9521808	0.9661084	0.9793599	1.0000000
0.9381880	0.9413465	0.9393227	0.9414484	0.9586847	0.9698278	0.9848786
0.9336140	0.9330056	0.9281905	0.9301548	0.9498871	0.9638331	0.9775429
0.9310289	0.9309882	0.9264741	0.9288885	0.9485362	0.9619393	0.9712373

Next

1234

Previous

1-10 of 31 rows | 1-7 of 31 columns

Os dados mostram uma tendência visível que varia de mais para menos conforme a variável se distancia da data em que o valor observado de fato ocorreu.

Embora neste recorte específico possamos perceber uma tendência relativamente linear, cabe ressaltar que diferentes fatores podem afetar as cotas, alguns linearmente relacionados e outros não, como a precipitação em pontos distantes que chegam aos rios por escoamento superficial e subterrâneo (CHOW et al., 1994 apud CAPOZZOLI et al., 2017).

As ferramentas utilizadas podem ser readaptadas para diferentes intervalos e tipos de conjuntos com poucas adaptações. Com isto a contribuição na criação de modelos documentáveis e transparentes também aparece como uma possibilidade interessante.

Bibliografia

• AGÊNCIA NACIONAL DE ÁGUAS. Sistema Hidroweb - Séries históricas. Brasília, 2018. Disponível em: https://www.snirh.gov.br/hidroweb/. Acesso em: 29 jun. 2023

• AGÊNCIA NACIONAL DE ÁGUAS. Levantamentos topobatimétricos e geodésicos aplicados na Rede Hidrometeorológica Nacional. Brasília, 2021. Disponível em: https://www.gov.br/ana/pt-br/assuntos/monitoramento-e-eventos-criticos/monitoramento-hidrologico/orientacoes-manuais/documentos/manual-de-nivelamento. Acesso em: 29 jun. 2023

• GUZMÁN, N. G. Modelagem para estimativa de dados faltantes em série de dados meteorológicos. Dissertação (Mestrado em Modelagem Computacional) — Nova Friburgo: Universidade do Estado do Rio de Janeiro, 5 abr. 2018.

• BRASIL. Poder Executivo. Lei Nº 9.984, de 17 de julho de 2000. Dispõe sobre a criação da Agência Nacional de Águas e Saneamento Básico. Brasília, DF: Poder Executivo, 2000. Disponível em: http://www.planalto.gov.br/ccivil_03/leis/l9984.htm

• R CORE TEAM. R: A language and environment for statistical computing. Vienna, Áustria. R Foundation for Statistical Computing, 2018. Disponível em: https://www.R-project.org/. Acesso em: 29 jun. 2023

• ALLAIRE, J. J. et al. Quarto. 23 jun. 2023. Disponível em: https://quarto.org/

• R CORE TEAM. cor: Correlation, Variance and Covariance (Matrices). Disponível em: https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/cor. Acesso em: 1 jul. 2023.

• CAPOZZOLI, C. R.; CARDOSO, A. DE O.; FERRAZ, S. E. T. Padrões de Variabilidade de Vazão de Rios nas Principais Bacias Brasileiras e Associação com Índices Climáticos. Revista Brasileira de Meteorologia, v. 32, p. 243–254, jun. 2017.

• Recursos relacionados

  • Portal de Dados Abertos da ANA
  • Sistema Nacional de Informações sobre Recursos Hídricos
  • Hidroweb v3.2.7
  • Serviço Geológico do Brasil: Hidrologia
  • Rede Hidrometeorológica Nacional - RHN